Introduction: Why Excel NPV Skill Matters
The Excel NPV skill practice is essential for finance professionals, business analysts, and students learning investment evaluation. Net Present Value (NPV) is one of the most powerful tools in financial modeling because it helps you determine whether future cash flows are worth today’s investment.
In this blog, we’ll explain what NPV is, why it matters, and provide 20 Excel NPV skill practice problems with solutions using real datasets. By the end, you’ll be confident in applying Excel’s NPV formula for loan schedules, investment analysis, and cash flow forecasting.
What This Article Covers
- What NPV means and why it matters in financial modeling
- Real-world scenarios of using NPV in Excel
- Example dataset for multiple projects
- 20 Excel NPV skill practice problems with solutions
- A downloadable practice file for hands-on learning
What Is Net Present Value (NPV)?
Net Present Value (NPV) measures the value of future cash flows discounted back to today. It accounts for the time value of money — the idea that money today is worth more than money in the future.
- Positive NPV → The project is profitable.
- Negative NPV → The project will cause a loss.
- Zero NPV → The project breaks even.
NPV Formula in Finance
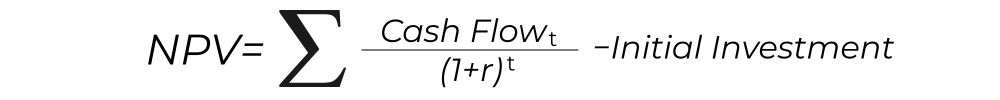
Where:
- Cash Flowâ‚ś = Cash inflow/outflow in year t
- r = Discount rate (cost of capital)
- t = Time period
In Excel, you calculate this using:
=NPV(rate, values)
(Note: Excel’s NPV assumes cash flows occur at end of each period. To include initial investment, subtract it separately.)
Example Dataset for NPV Practice
We’ll use the following dataset for projects A, B, and C:
| Project | Year | Cash Flow | Discount Rate |
|---|---|---|---|
| A | 1 | 10,000 | 10% |
| A | 2 | 12,000 | 10% |
| A | 3 | 15,000 | 10% |
| B | 1 | 8,000 | 12% |
| B | 2 | 9,000 | 12% |
| B | 3 | 11,000 | 12% |
| C | 1 | 20,000 | 8% |
| C | 2 | 25,000 | 8% |
| C | 3 | 30,000 | 8% |
20 NPV Excel Skill Practice Problems with Solutions
Here are 20 NPV practice problems with step-by-step solutions:
1. NPV for Project A (10%)
Formula: =NPV(10%,C2:C4)
Answer: 30,277.99
2. NPV for Project B (12%)
Formula: =NPV(12%,C5:C7)
Answer: 22,147.18
3. NPV for Project C (8%)
Formula: =NPV(8%,C8:C10)
Answer: 63,766.96
4. Project A with $20,000 initial investment
Formula: =NPV(10%,C2:C4)-20000
Answer: 10,277.99
5. Project B with $25,000 initial investment
Formula: =NPV(12%,C5:C7)-25000
Answer: -2,852.82
6. Project C with $50,000 initial investment
Formula: =NPV(8%,C8:C10)-50000
Answer: 13,766.96
7. Compare NPVs – highest project
Answer: Project C (63,766.96)
8. Project A at different discount rates
- 10% → 30,277.99
- 12% → 29,171.60
- 15% → 27,632.12
9. New Project D (5 years: 5000, 6000, 8000, 9000, 12000 @10%)
Answer: 29,112.83
10. Irregular cash flows (Year1=10000, Year3=15000, Year4=20000 @10%)
Answer: 34,020.90
11. Cumulative NPV (Projects A+B+C)
Answer: 116,192.13
12. NPV with negative Year 2 cash flow (12000, -5000, 15000 @10%)
Answer: 18,046.58
13. Project A with terminal value of 10,000 in Year 3
Answer: 37,791.13
14. Monthly cash flows (100, 200, 300 @12% annual → 1% monthly)
Answer: 586.25
15. Quarterly cash flows (1000, 2000, 3000 @12% annual → 3% quarterly)
Answer: 5,601.49
16. Break-even IRR for Project A (initial -20000, inflows 10000, 12000, 15000)
Answer: 35.31%
17. 10-year cash flows of 1000 each @10%
Answer: 6,144.57
18. Compare NPV vs raw sum of Project A
- Sum = 37,000
- NPV = 30,277.99
19. Project C converted to USD (rate 0.013)
Answer: 828.97
20. Scenario Analysis for Project A
- Optimistic (+10% flows) = 33,305.79
- Pessimistic (-10% flows) = 27,250.19
Why NPV Matters
- Helps in making informed investment decisions
- Considers time value of money (unlike simple totals)
- Enables comparison across projects with different durations
- Forms the foundation of advanced valuation models like IRR and DCF
Final Thoughts: Strengthen Your NPV Excel Skill for Career Growth
The Excel NPV skill practice is a must-have for anyone working with financial data. By understanding and applying NPV, you can evaluate investment projects, compare scenarios, and make better financial decisions.
Practice these 20 problems, and you’ll not only sharpen your Excel skills but also improve your financial decision-making confidence.
Related Topics
- EDATE Skill Practice – Shifting dates by months (loan maturity, billing cycles).
- EOMONTH Skill Practice – Finding month-end dates for cash flow forecasts.
- TODAY / NOW Skill Practice – Using dynamic current date/time in aging reports.
- TEXT Skill Practice – Formatting numbers, dates, and percentages professionally.
- CONCAT / TEXTJOIN Skill Practice – Combining text strings for reports and IDs.
